2024/01/22ARCUS奥戸CSNew!
【2024市川中】算数入試解説/大問5
2024年 市川中 算数 大問5
※難易度 ★・★★・★★★・★★★★の四段階
大問5 ニュートン算の応用といもづる算
(1)★★〜★★★
(2)★★★
(3)★★★
【所感】(1)は少し捻ったニュートン算、(2)は条件整理を工夫するいもづる算、(3)は(2)から指定の条件を探す思考力問題でした。
<解説>
(1)ニュートン算の解き方はいくつかありますが、今回は以下の図を用いて解きました。
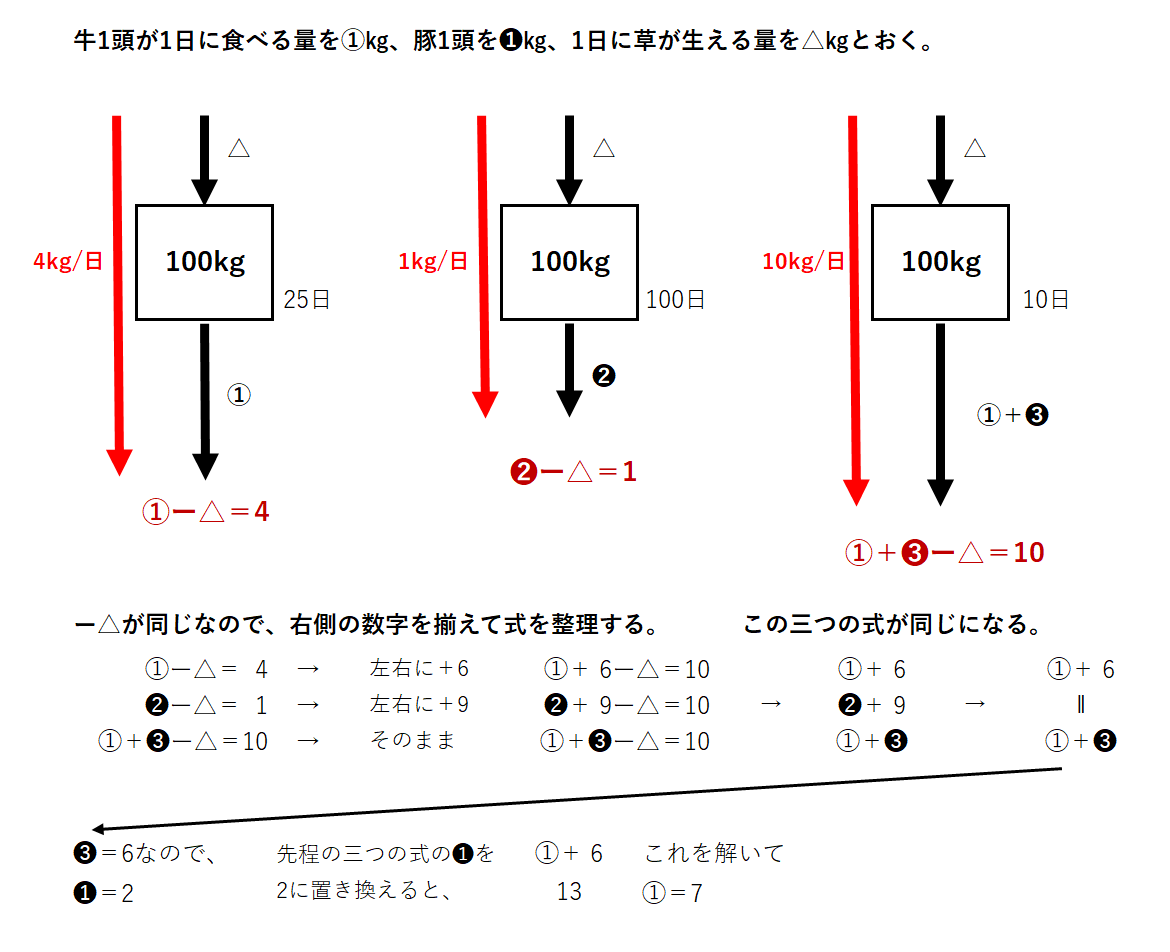
よって、牛:7s 豚:2s
(2)(1)より、草が1日に生える量は3s/日ということがわかる。
次に「牛1・豚1がいて、毎日最低1頭」という条件を考えると、@牛1頭 A豚1頭 B牛1頭・豚1頭の3パターンが考えられる。
それぞれのパターンで1日に食べる草の量は、
@牛1頭=7s A豚1頭=2s B牛1頭・豚1頭=9s
1日に3s草が生えることを考慮すると、実際に1日に減らせる草の量は生える3sを差し引いて、
@牛1頭=4s A豚1頭=-1s B牛1頭・豚1頭=6s となる。
@ABで合わせて22日で合計100kgを食べる、これはいもづる算になるのだが、このままだと−があるため計算しづらい。そこで、22日分の草の生える量=3×22=66sを最初から足しておいて、166sの草を @牛1頭=7s A豚1頭=2s B牛1頭・豚1頭=9s の3通りの組み合わせから考えるようにすると通常のいもづる算となる。
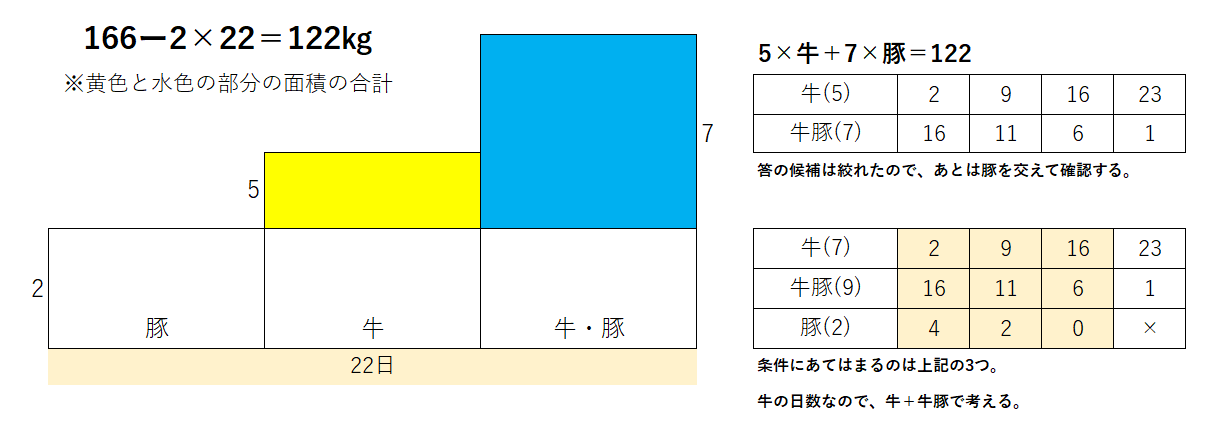
よって、牛が放たれた日数は、2+16、9+11、16+6となり、
18日、20日、22日
(3)(2)より、牛が放たれた最も少ない日数は18日。この時、牛2日、牛豚16日、豚4日となるので、
A×16、B×2、C×4 となる。
ここで改めて本問題の条件を確認すると、
・1日3sずつ草が生える
・最初の量は100s
よって減らす量が100sを超えてはいけないので、A(牛豚9s/日)は実質1日9-3=6s減らすため、16日連続までしか食べてはいけない。またB(牛7s/日)は実質1日4s減らし、C(豚2s/日)は実質1日1s増やす。よって、A×16=96s減、B×2=8s減、C×4=4s増となり、22日目まで草が残らないといけないので、
A×16→C×4→B×2
C×4→A×16→B×2
C×4→B×2→A×16
B×2→C×4→A×16
※いずれかでOK
以上でした!
塾長 鴨志田
***** お知らせ *****
算数専門のオンラインプロ個別「Vise(ヴィゼ)」を新設しました。
各大手塾の算数対策や、プロによる過去問指導をご希望される方は、
ぜひ一度お問合せください。
詳細はこちらから。










