2024/01/22ARCUSNew!
【2024市川中】算数入試解説/大問４
２０２４年 市川中 算数 大問４
※難易度 ★・★★・★★★・★★★★の四段階
大問４ 時計算（長針逆回転＆なす角を二等分）
（１）★★
（２）★★★
（３）★★★
【所感】長針が逆回転する時計算。しかも、長針・短針・6を指す動かない針でのなす角の二等分を扱った問題。時計算は苦手な子も多く、しかも「長針逆回転＋なす角二等分」の組み合わせで、あかん…となった子も多かったのでは？(1)は普通に計算するだけで、落ち着いて解けば大丈夫。鬼門は(2)で、脳内で針を動かして考えるのが早いのだが、答である「Y→Z→X→Z→Y→Z」の2番目のZを見落としやすく、それを落とすと(3)も落とすという負の連鎖問題。
＜解説＞まず三つの状態があるのでおさらい。
①状態X（AがLとSのなす角を二等分）
②状態Y（SがLとAのなす角を二等分）
③状態Z（LがAとSのなす角を二等分）
（１）８時から時計を動かして、初めて状態Xとなるのは以下の図の時。図１が８時から考えるスタンダードな解き方で、図２は９時から時間を巻き戻して考える解き方。
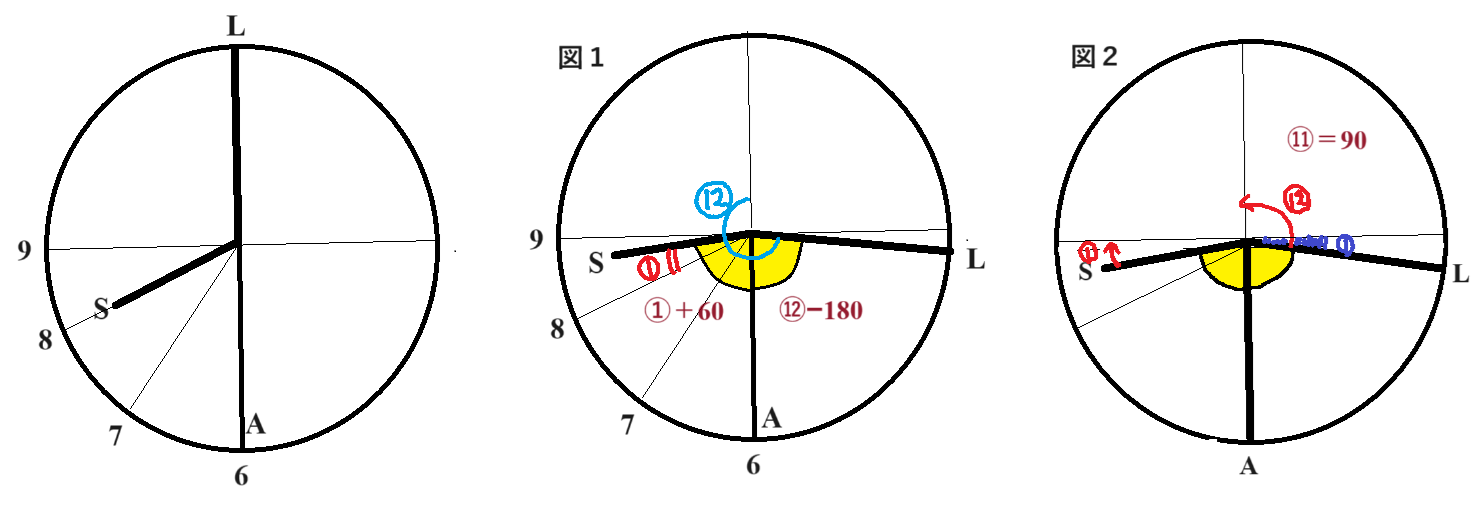
【図１での解き方】
長針のなす角：短針のなす角＝⑫：①を利用し、二等分された角をそれぞれ式で表すと、
①＋60＝⑫ー180
⑪＝240
①＝240/11
よって、8時から短針が240/11度進んだ時間が求める時間となるので、
240/11÷0.5＝480/11＝43と7/11分
【図２での解き方】
9時から短針が①、長針が⑫巻き戻ったと考えると、図より、
⑫ー①＝90
⑪＝90
①＝90/11
よって、9時より90/11度巻き戻った時間となるので、
90/11÷0.5＝180/11分前
60分ー180/11分＝480/11＝43と7/11分
（２）8時から順々に丁寧に考えましょう。以下の図となります。
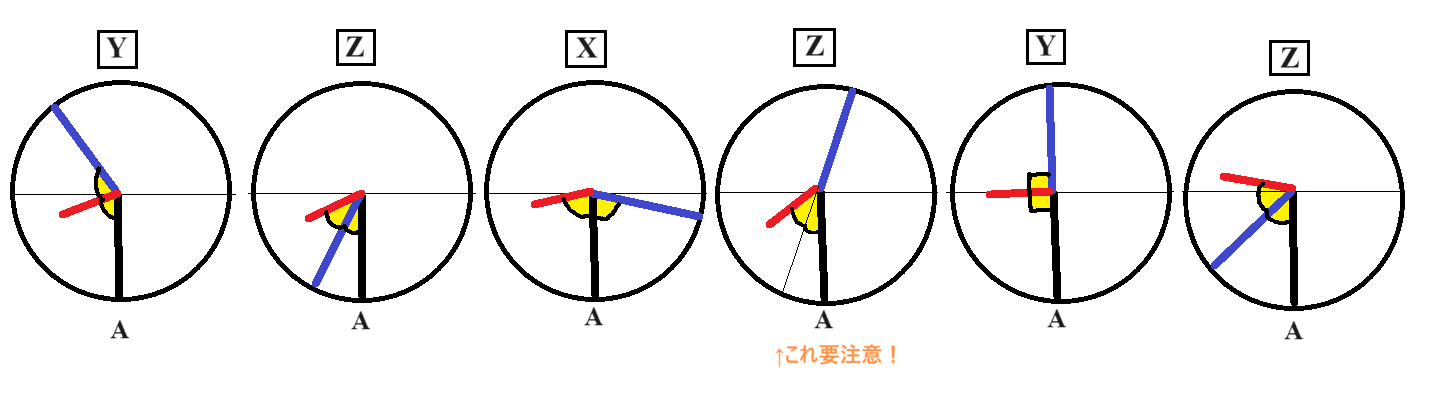
Y→Z→X→Z→Y→Z
2回目の状態Z、要注意です。反対側の角度の二等分にも気をつけましょう！
（３）2回目の状態Zは9時前になるので、9時から時間を巻き戻して考える。
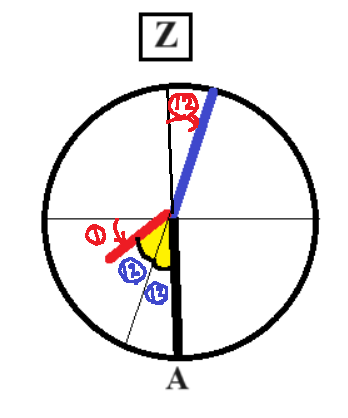
(25)＝90度
①＝3.6度
3.6÷0.5＝7.2分
よって、9時から7.2分前の8時52.8分となる。
52.8分後
でした！
塾長 鴨志田
＊＊＊＊＊ お知らせ ＊＊＊＊＊
算数専門のオンラインプロ個別「Visée（ヴィゼ）」を新設しました。
各大手塾の算数対策や、プロによる過去問指導をご希望される方は、
ぜひ一度お問合せください。
詳細はこちらから。
