※難易度 ★・★★・★★★・★★★★の四段階にしました
大問4 場合の数(コマが碁盤上を移動する)
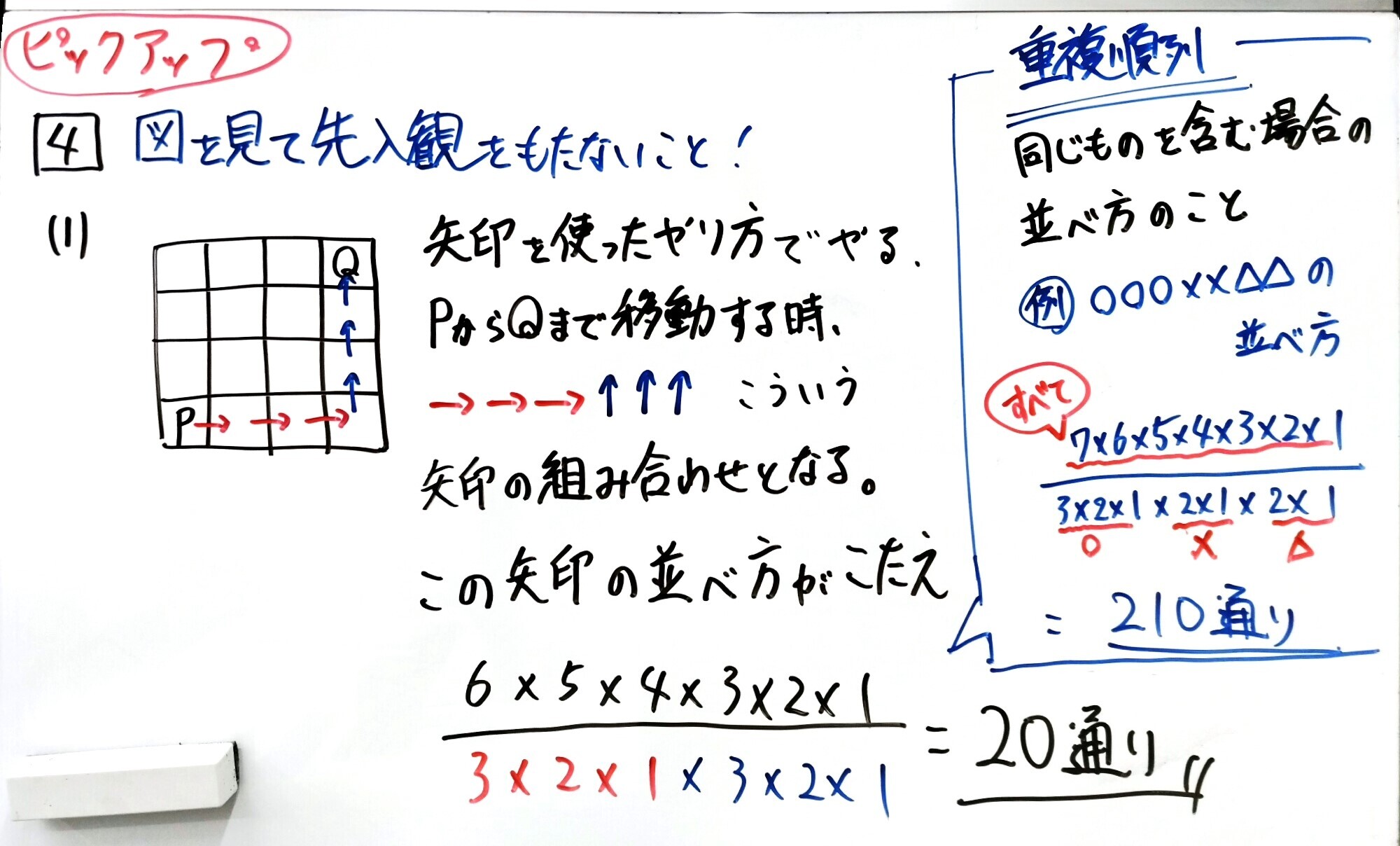
★(1)コマAが端から端まで移動する行き方
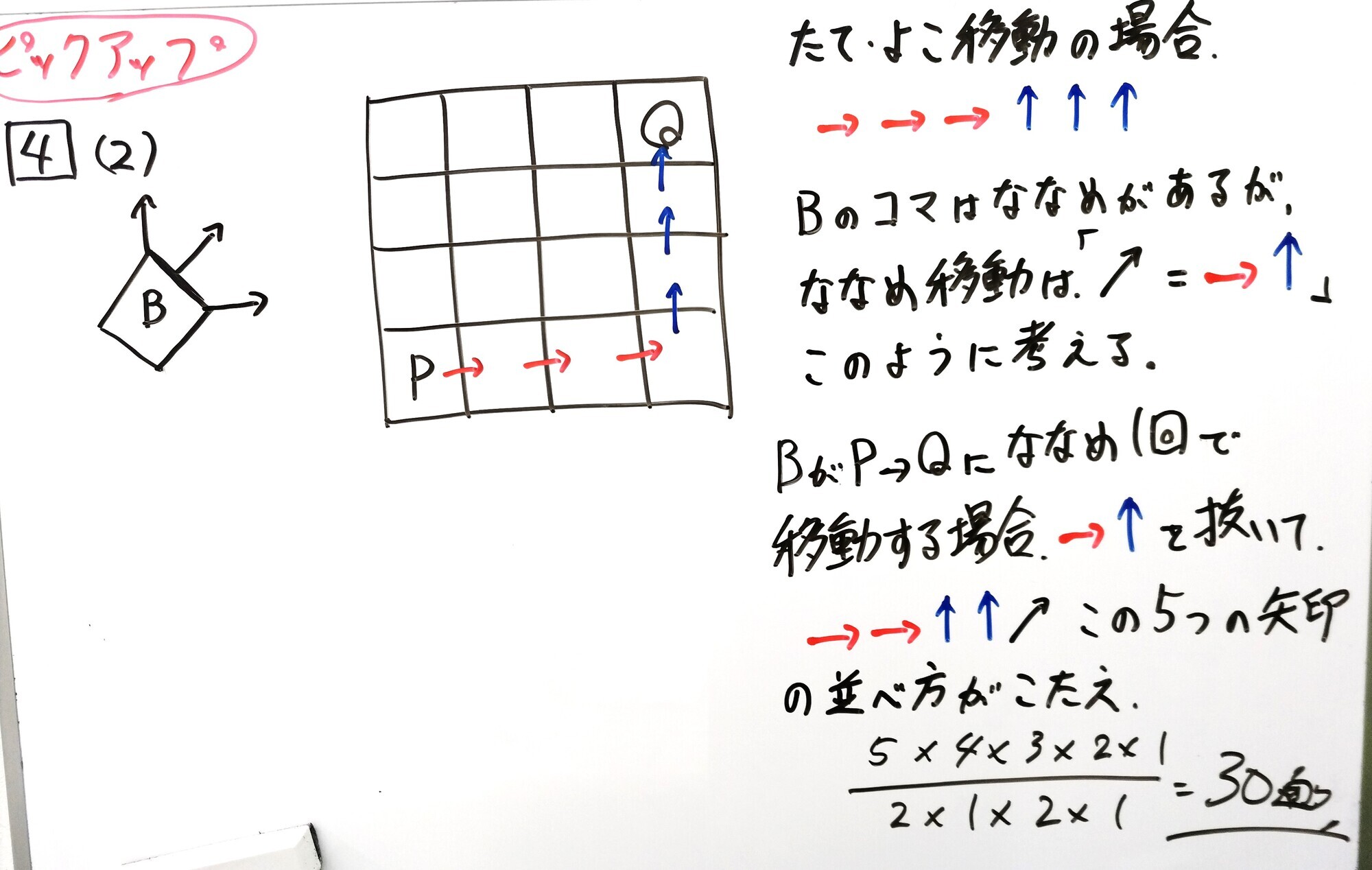
★★(2)コマBがななめ移動を伴う行き方
★★(3)(1)(2)を利用したコマBの移動の全通り
【所感】ちょっとしたひっかけ問題で、マス目の正方形を見た瞬間に「最短距離の問題だ!」と思って早とちりすると、雪崩式に全滅する問題。線上を移動するわけではなく、マス目上を移動します。ここがひっかけポイント。見た目の図の思い込みで解くと痛い目を見るので、気をつけましょう。
<解説>
★(1)コマAが端から端まで移動する行き方
問題を理解すれば簡単に正解できる問題。本問はマス目上を移動するため、4×4の図形が書いてありますが、実際は3×3のマス目を移動するのと同義です。最短距離の問題はマス目の外に数字を振るやり方もありますが、矢印の組み合わせで考える方がお勧めです。それから「重複順列」の計算方法をしっかり理解しておきましょう(以下、補足あり)
★★(2)コマBがななめ移動を伴う行き方
ななめ移動をどう捉えるか?「=→↑」という仕組みに気づけば、あとは矢印を置き換えるだけ(以下、補足あり)
★★(3)(1)(2)を利用したコマBの移動の全通り
誘導に気づけば、移動の回数で場合分けしておしまい(以下、補足あり)

大問5 フィボナッチ数列と周期算
★(1)2の倍数を求める周期算
★(2)5の倍数を求める周期算
★★★(3)40の倍数を求める周期算
【所感】フィボナッチ数列+周期算、という問題。(1)(2)は書き出してゴリ押して解いてほしい。(3)は上手に誘導に乗り切れれば解答可能。気づきにくいかな、という点で★★★にしました。
<解説>
★(1)2の倍数を求める周期算
★(2)5の倍数を求める周期算
もっと先の数列まで書き出して、2の倍数に〇していけば周期に気づくはず…(以下、補足あり)

★★★(3)40の倍数を求める周期算
(1)(2)の誘導にどう乗るか。2の倍数と5の倍数が周期になっていることがわかったので、他の倍数も調べてみる。そして2の倍数の周期、3の倍数の周期、6の倍数の周期を見てみると、6は2と3の周期の重なりであることがわかる。”公倍数周期”みたいな感じで捉えてもらえば。であれば、40の倍数は5の倍数の周期と8の倍数の周期の重なりとなるので、5の倍数が1周期「5こ」、8の倍数が1周期「6こ」、よって40の倍数は1周期「30こ」(以下、補足あり)


*****
以上で解説は終了となります。
1/16のB日程、リベンジする方はぜひ頑張ってくださいね!!
塾長 鴨志田










