2023/01/09ARCUSNew!
【超速報】2023年SAPIX/新6年組分けテスト（算数解説＋所感）
＜重要＞解答は見ましたが解説は見ていませんので、模範の解説と異なる部分がたくさんあるかもしれません。その点ご容赦ください！
２０２３年 ＳＡＰＩＸ新６年組分けテスト 算数 解説と所感
※難易度 ★・★★・★★★・★★★★の四段階にしました
大問１ 計算
★（１）かっこのある計算
★（２）分数計算
★（３）□のある計算
【所感】SAPIX生はノーミスで全問正解必須の問題でした。あえて強弱つけるなら、（３）がやや正答率低いかもしれません。
大問２ 小問集合
★（１）時計算（5:33の長針と短針の作る角度）
→落ち着けば難しくない問題。ちゃんと時計の絵を描いて解こう。
★（２）硬貨の組み合わせ（270円の組み合わせ方）
→王道の問題です。ミスなく書き出しましょう。
★（３）分子が指定された既約分数（5/16～6/13の範囲で、分子が9の既約分数を探す）
→分子の通分を知っていれば秒殺。ただし既約分数なので、あてはまらないものを最後に抜くこと
★★（４）旅人算（向かい合って進み、片方が引き返した後に追いつかれる）
→ダイヤグラムよりも線分図で状況整理し、結局二人が出会うまでに二人で合わせて1600m進んでいることがわかれば、1600÷（70+80）＝32/3分＝10分40秒 で終了。ダイヤグラムや比で、下手にこねくり回す方が遠回りになる問題
★（５）組み合わせ（5枚⇒3枚ならべてできる3桁の3の倍数）
→3の倍数判定法を知らないサピ生はいないと思うので、(0,2,4)(0,4,8)(2,4,6)(4,6,8）を選び、（）内での並べ方を求めて20通り
★（６）濃度算（食塩水の取捨問題）
→普通に計算だけで順序立てて解く問題。下手にひねって考えず、面積図・てんびん図も使わない方が早い。
12%/200g(24) → 12%/150g(18) → 10%/180g(18)
→ 10%/160g(16) → 8%/200g(16)
※操作系食塩水含めた濃度算は、「変わらないもの」に注目して状況整理すること
【所感】難しそうに見えて難しくない問題、といった印象でした。ここも全問正解必須ですが、1問は落としてもしょうがないかなと思います。
大問３ 図形小問集合
★★（１）等積利用の辺の長さ（台形を等積分割する）
→慣れてる方は比でパパっと解ける問題。また夏頃にやるので、このパターンは要履修（以下、補足説明あり）
★（２）円の中の斜線部の求積（面積移動）
→右下と左下のおうぎ形を反対側に移動させて、なるべく一か所に集めて計算で解く
★（３）積み木と表面積（平面図での整理）
→前後・上下・左右から見える平面図をそれぞれ描き、求めましょう
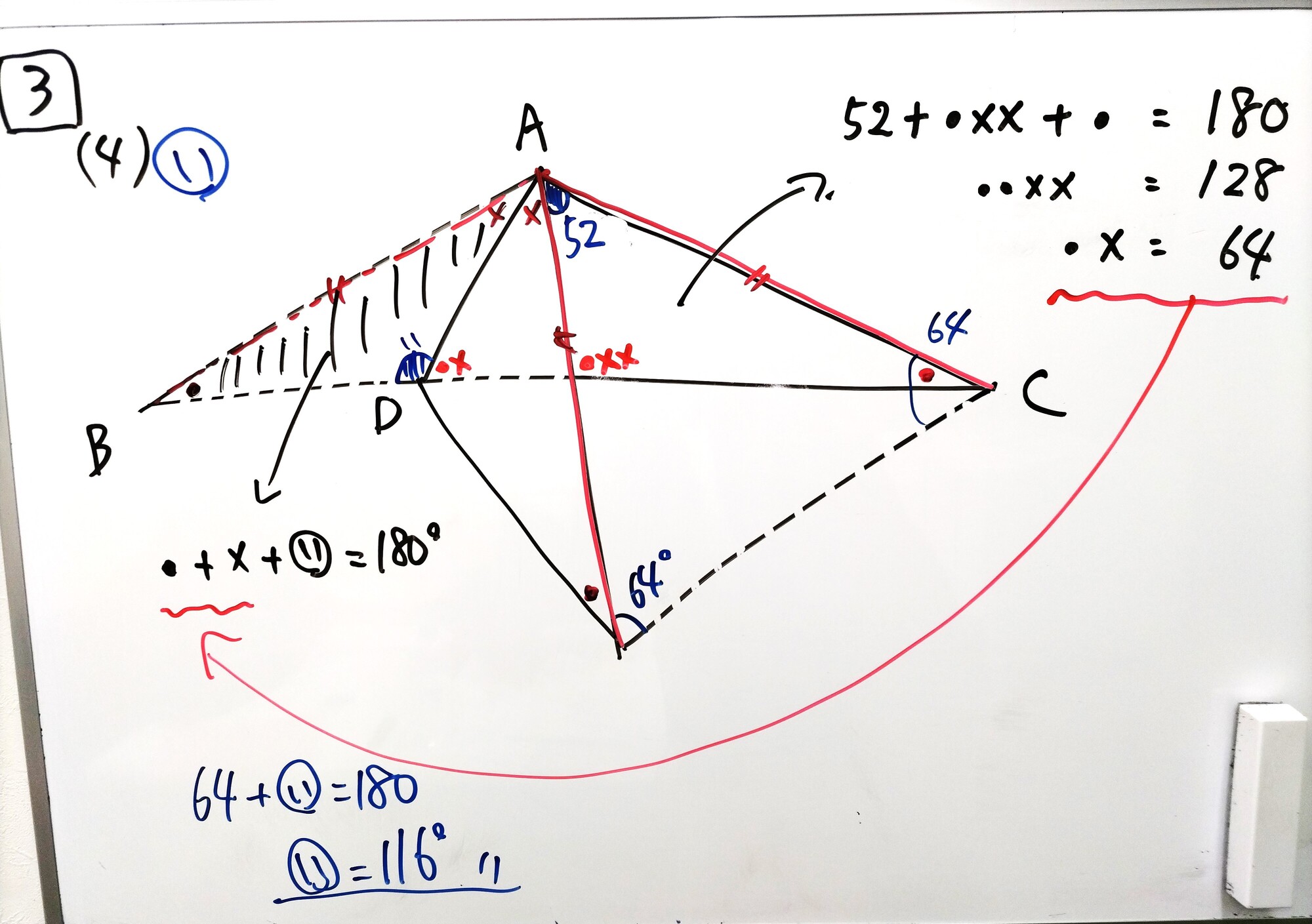
★★（４）二等辺三角形と折り返し（求角の●×利用）
→「あ」はすぐに求められるはず。問題は「い」ですが、折り返しの求角で定石でもある”同じ部分を●×でおく”やり方で解決できる問題（以下、補足説明あり）
【所感】★・★★は四問の中で強弱をつけた結果なので、見方によってはすべて★でもよいと思います。
【補足解説】
★★（１）等積利用の辺の長さ（台形を等積分割する）
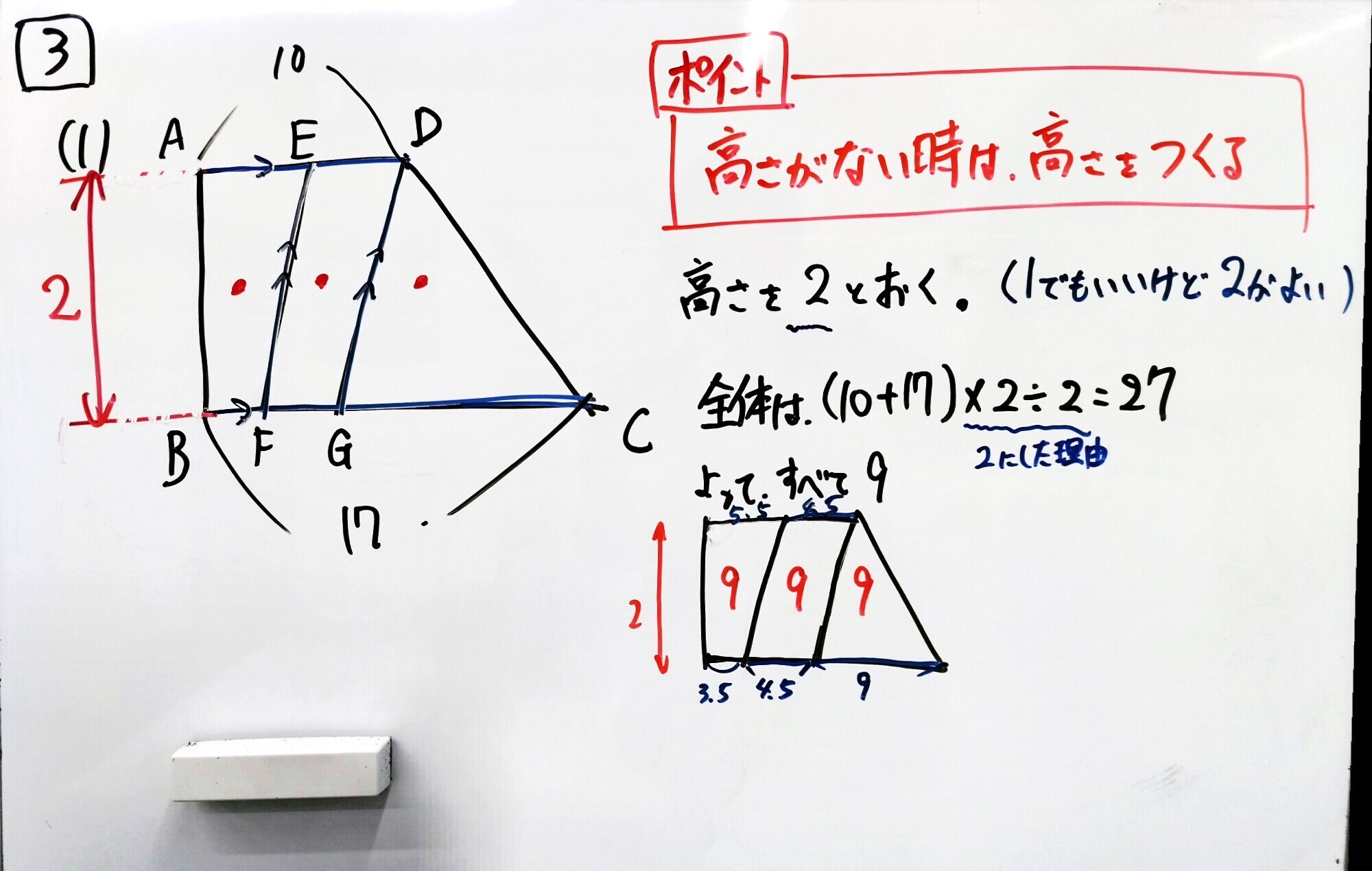
高さを数字でおいて、そこから面積を出して順々に長さを出していくのが良いかなと思います。
★★（４）二等辺三角形と折り返し（求角の●×利用）
大問４ 売買算
★（１）利益の総額（むしろ設問理解）
→条件整理をしっかり。＜仕入値：18円 定価：30円 閉店1時間前：24円＞。85個は定価売り、15個は24円売り。
★（２）仕入個数（ただの条件整理）
→24円で売った20個の利益は、(24-18)×20＝120円 定価で売った利益の合計は、1056円ー120円＝936円。定価で売った時の利益は1個12円なので、定価で売った個数は、936÷12＝78個 よって仕入個数は、78+20=98個
★★（３）売れ残りがある時の個数（面積図利用）
→売れ残り（廃棄）がある場合の典型問題。面積図で条件整理し、「仕入＋利益＝売上」という式を理解していれば簡単に解ける問題。（以下、補足説明あり）
【所感】これも標準レベルの問題。解き慣れている子はすんなり解けたはず。タイムセールの設定で少し捻っている感を出してはいるが、売買算の中でも比較的簡単なレベルだと思われる。
【補足説明】
★★（３）売れ残りがある時の個数（面積図利用）
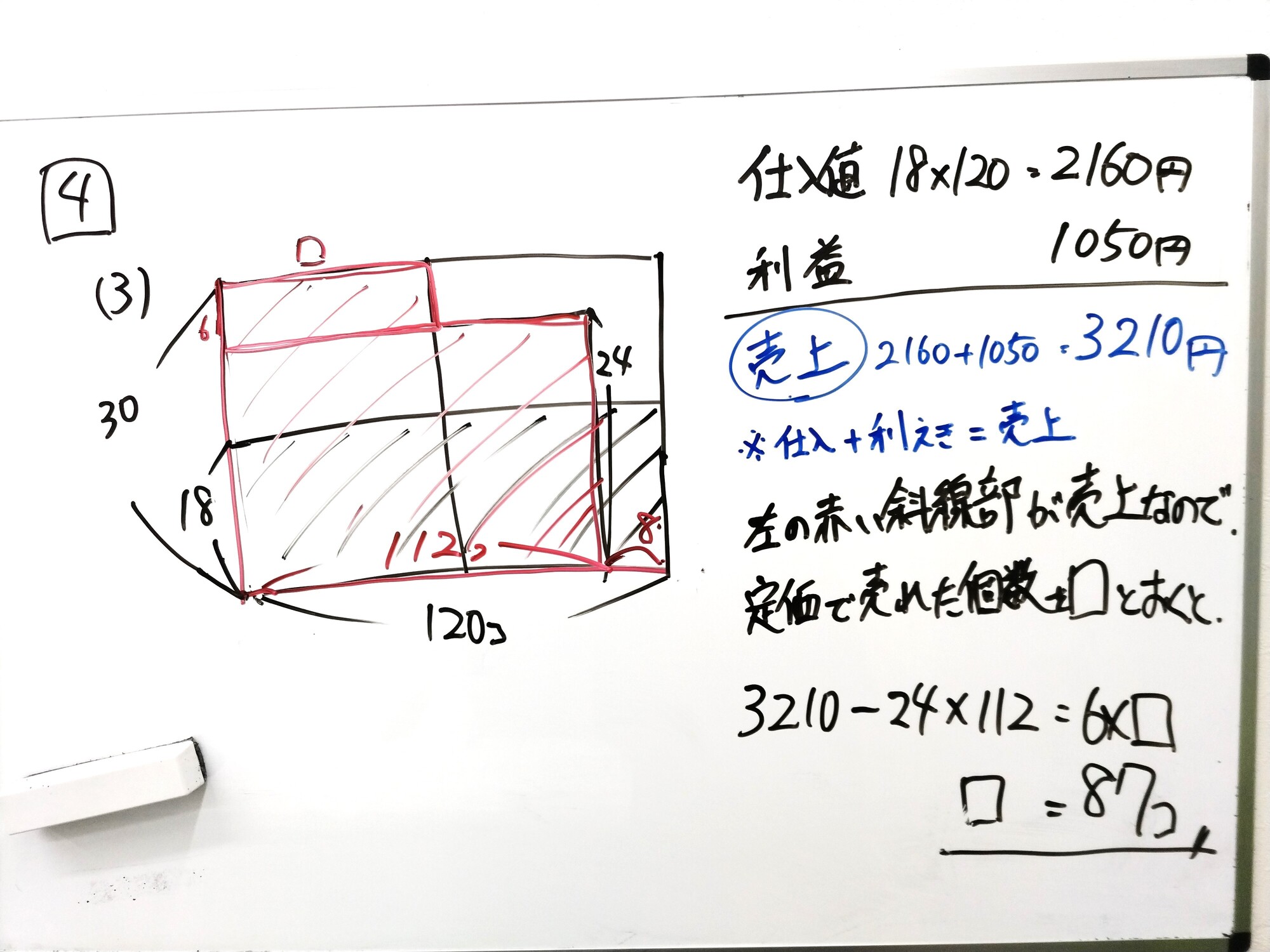
大問５ 規則性
規則は3つの並びを1グループとし、（〇、〇×2、〇×３）という規則。
★（１）40番目の数（周期算）
→規則の理解あれば簡単。40÷3＝13…1 これより、14グループ目の最初の数が求める数とわかる。1グループ目の最初の数は1、2グループ目の最初の数は2、よって14グループ目の最初の数は「14」
★★（２）24は何個ある？（規則の正しい理解）
→一つのグループ内の規則は前述した通り、（〇、〇×２、〇×３） 24が3個あるのは、〇＝24、〇×2＝24、〇×3=24の三つのパターンがあるから。
〇＝24の時、24は（24,48,72）の中にある
〇×2＝24の時、〇＝12となるので、24は（12,24,36）の中にある
〇×3=24の時、〇＝8となるので、24は（8,16,24）の中にある
順々に考えると、(1,〇,〇)…(8,16,24)…(12,24,36)…(24,48,72)…となり、あとは何番目かを考えるだけ。
(8,16,24)は、(1,〇,〇）（2,〇,〇）（3,〇,〇）（4,〇,〇）（5,〇,〇）（6,〇,〇）（7,〇,〇）（8,16,24）←ここにいる
3×7＋3＝24番目
同じ方法で考えると(12,24,36)は、3×11＋2＝35番目
(24,48,72)は、3×23＋1＝70番目
★★★（３）前問の応用問題（範囲の指定）
→（２）が出来ていれば出来るかな。
まず100番目までの数の並びは、100÷3＝33…1より、（1,〇,〇）（2,〇,〇）…（33,〇,〇）（34）まで。この規則のルールは（〇、〇×２、〇×３）なので、同じ数が３つある条件は、どこかの〇＝どこかの〇×２＝どこかの〇×３になる時のみ。すなわち2の倍数かつ3の倍数となり、今回求める数は「６の倍数」となる ←ここちょい難しいかな？34までの6の倍数で、かつ24を除けば答なので、6,12,18,30
【所感】この手の問題を見たことがない子は戸惑って解けなかったかも。ただ小6SAPIX生を教えている感覚で言うと、「これぐらい余裕でしょ？」になってしまうので、今は難しく感じても、これを応用レベルに位置付けないでほしい、というのが率直な感想。
大問６ 動点とグラフ
★（１）グラフの読み取り
→グラフで秒数がわかっているのは4秒後なので、4秒後の面積を考えてみる。Qは8㎝動いており、右下の△BCQ＝24、正方形ABCDの面積は144。よって4秒後に□PBQDが120になる条件は、PがAにいること。ゆえにPは4秒で12㎝移動したので、12÷4＝3㎝/秒
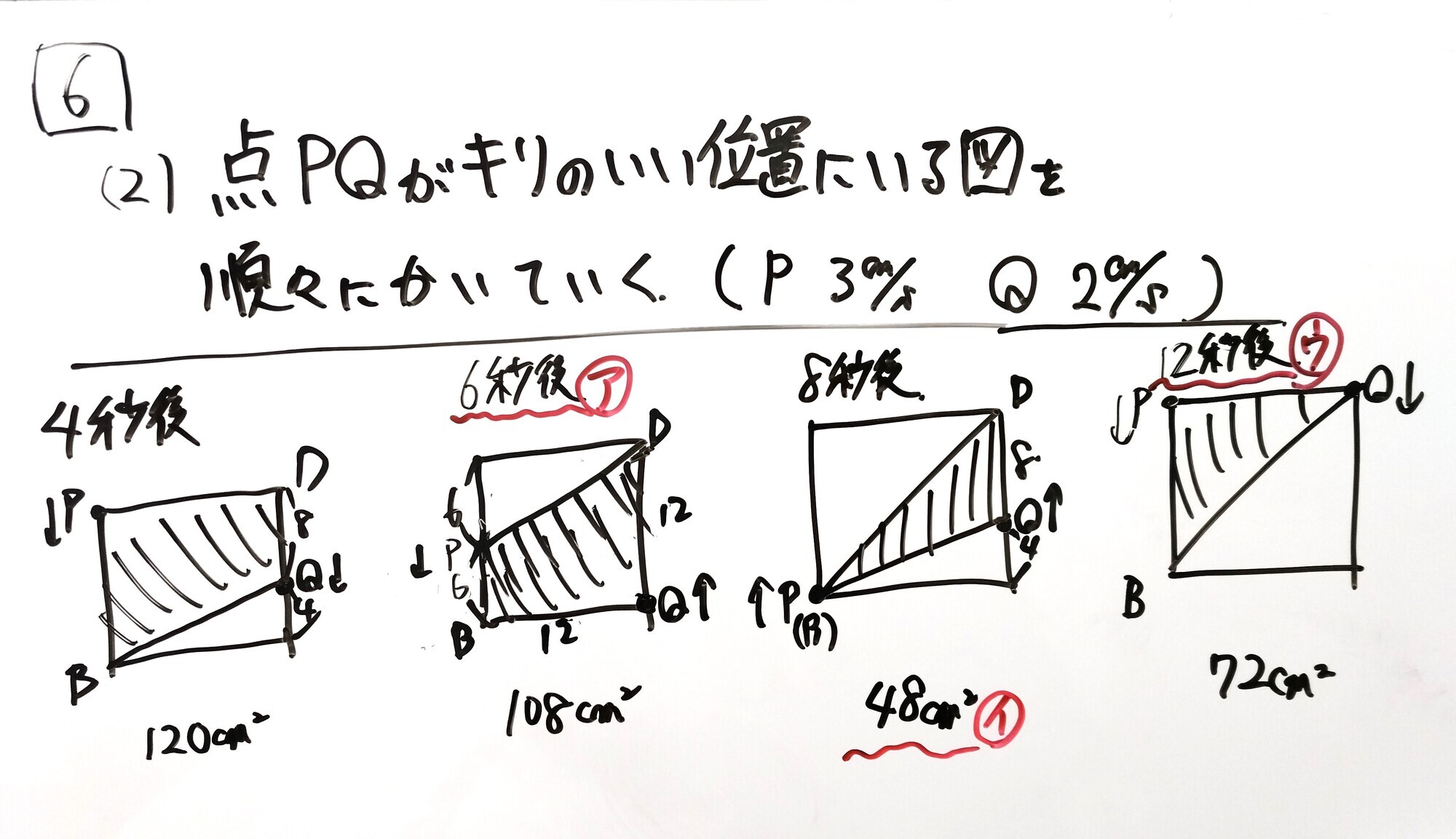
★★（２）点の移動後の図形への正確な理解
→二点動く場合は、それぞれの点がキリのいい位置に移動した図を、順を追って書いていくのが正攻法。（以下、補足説明あり）
★★★（３）面積が半分になる時（前問の続きからの応用）
→（２）の続きを描くのだが、マルイチ算をうまく利用して解くところがミソ。これは地力の差が出そうな問題。（以下、補足説明あり）
【所感】動点と面積のグラフという、ジャンルとしては王道の問題。50分という時間制限のある組分けテストの大問6で、現小5が解くという色眼鏡で見れば、多少難しいかなという印象。問題単体で見れば、解き筋にそこまで難しい考え方は求められていないため、(1)(2)はすんなり解けてほしい。(3)も偏差値60以上だったら解けなきゃだめ。
【補足説明】
★★（２）点の移動後の図形への正確な理解
★★★（３）面積が半分になる時（前問の続きからの応用）
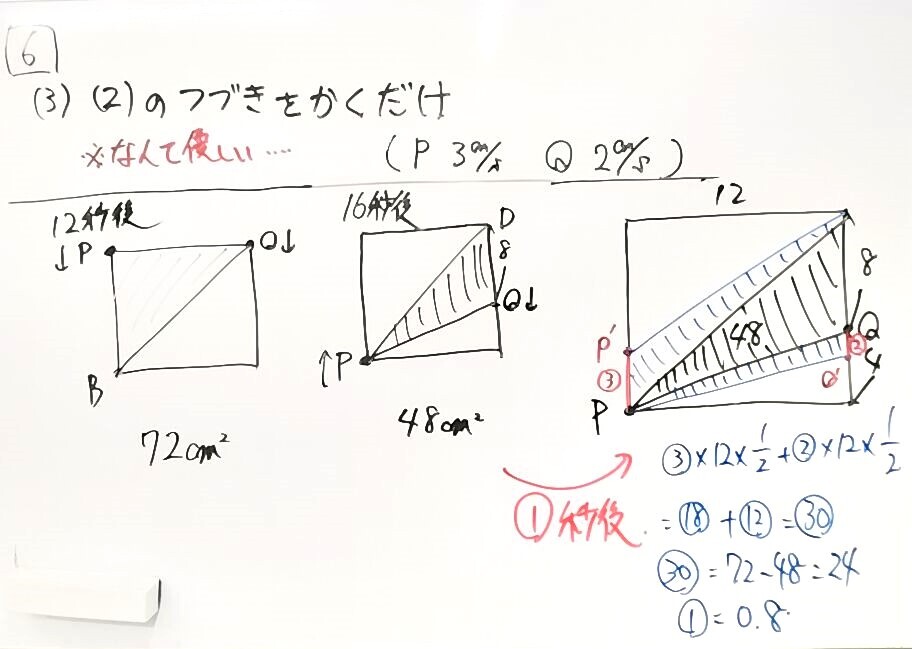
よって、16+0.8=16.8秒後
大問７ 思考力問題（コラッツ予想、2021慶應中等部入試問題の大問５）
知る人ぞ知る？コラッツ予想、近年だと中等部の入試で出題されました。一度解いた経験の有無がかなり大きい問題。
★（１）ひたすらにルールに沿って書いていく問題
→（奇数＋１）×２、偶数÷２、このルール通りに書き出していくだけ。時間切れでここまでたどり着けなかった子はもったいなかったです
★★★（２）ルールの延長
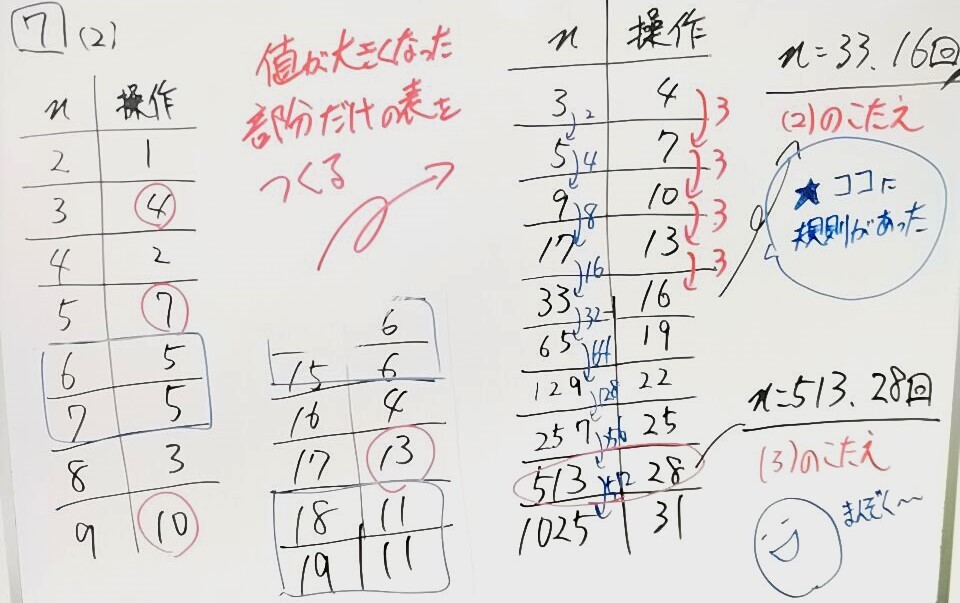
→書き出すか？規則を見つけるか？nは偶数より奇数の方が操作回数は多くなるので、31,33,35あたりに操作を行いゴリ押しするのも悪くはないですが、それだと（３）は絶対解けません。ここで規則を見つけられれば、実は(2)(3)はセットで解けます…（以下、補足説明あり）
★★★★（３）ルールの一般化
→規則を見つけられれば実は簡単な問題ですが、ハードルは激高だと思われます…。操作回数が大きくなる部分だけに着目して表で整理すると、実は規則がありました…（以下、補足説明あり）
【所感】まさかコラッツ予想を出すとは…。組分けの最後の問題は、慶應中等部2021過去問の大問5の＋αでしたね。だったら次は図形の三角形分割（カタラン数）が出る？？とか思ったり(笑)。非常に良問でした、面白かった！解説読んでないので、ちょっと戦々恐々としています…。50分内でこれを解くのはさすがに厳しいです！！
【補足説明】
★★★（２）ルールの延長
★★★～★★★★（３）ルールの一般化
以上で解説終了となります。お疲れさまでした！はい、疲れました！
最後の問題は、操作回数が同数になる部分に規則があるのかと最初は思いましたが、それだと答を導けなかったので、であれば操作回数が跳ね上がる部分にヒントがあるのでは？という発想で表整理して規則探しをしました。今回はそれが刺さりましたが、この問題にはもう少し数学的な解釈があると思います。ですがそれを小学生に求めても…と思い、規則は規則としてパズル的解法にて終局しました。
平均点予想はあまり好きではありませんが、80点前後だと思います！多分！
次回３月の組分けに向けてですが、自分の中ではこういう対策が良いだろうというビジョンが見えたので、それをやってみたいと思います。そしてそれは秘密です(笑)
（2023.04.07追記）
SAPIX生専用のコースを新設しました。まずはせひ一度ご覧になってみてください。
※こちらのボタンをクリック
塾長 鴨志田
＊＊＊＊＊ お知らせ ＊＊＊＊＊
算数専門のオンラインプロ個別「Visée（ヴィゼ）」を新設しました。
各大手塾の算数対策や、プロによる過去問指導をご希望される方は、
ぜひ一度お問合せください。
詳細はこちらから。
